논문 정보: Li, Z., Wang, W., Li, H., Xie, E., Sima, C., Lu, T., … & Dai, J. (2022). BEVFormer: Learning Bird’s-Eye-View Representation from Multi-Camera Images via Spatiotemporal Transformers. arXiv preprint arXiv:2203.17270.
이번에 리뷰할 BEVFormer 라는 논문은 2022년도 ECCV에서 발표된 논문입니다.
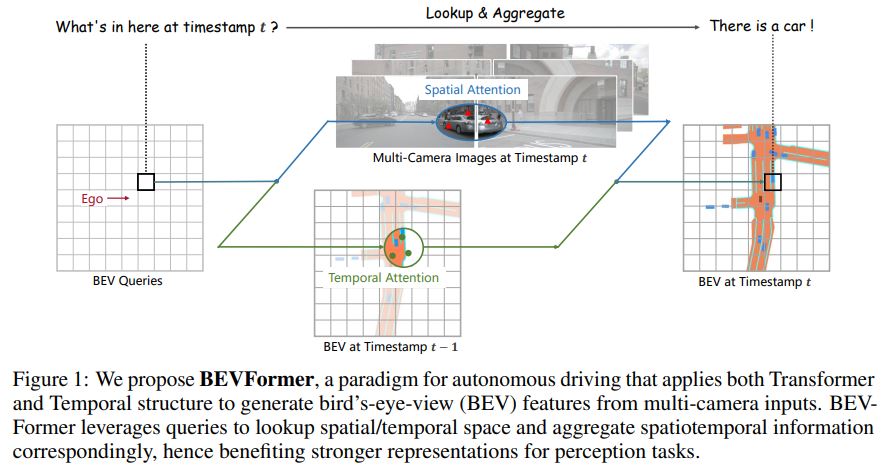
BEVFormer의 key design은 다음과 같습니다.
1) Grid-shaped BEV queries to fuse spatial and temporal features via attention mechanisms flexibly
2) Spatial cross-attention module to aggregate the spatial features from multi-camera images
3) Temporal self-attention module to extract temporal information from history BEV features, which benefits the velocity estimation of moving objects and the detection of heavily occluded objects.
BEVFormer
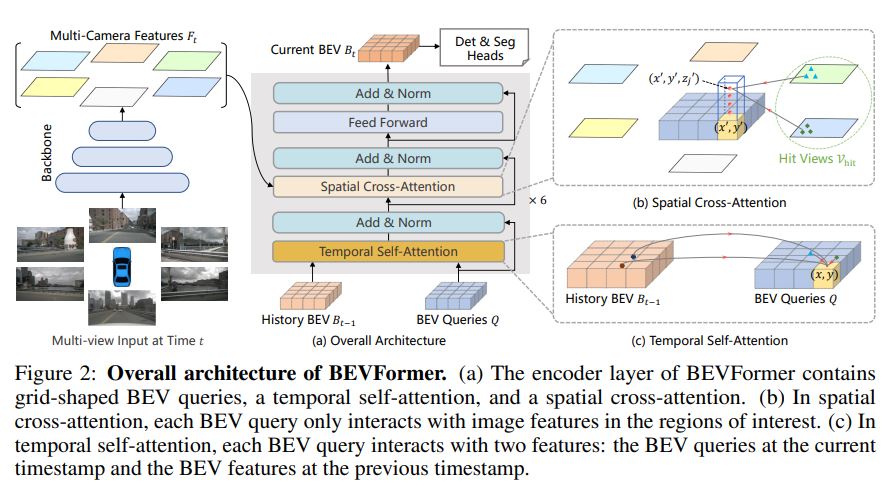
3.1 Overall Architecture
BEVFormer에 사용된 6개의 encoder layer는 기존 transoformer의 encoder와는 BEV query, spatial cross-attention, temporal self-attention의 3가지 design이 추가되었다는 점이 다릅니다.
BEVFormer의 대략적인 파이프라인은,
- T 시점에서, multi-camera image를 ResNet-101+FPN(1/16, 1/32, 1/64)로 feed, 6개의 feature를 얻음.
- 각 encoder에서, BEV queries로 t-1 시점의 BEV feature Bt-1으로부터 temporal self-attention으로 temporal information을 쿼리
- BEV queries로 multi-camera feature Ft로부터 spatial information을 Spatial Cross-Attention으로 찾음.
- 이 과정으로 refined BEV features를 만들고, 다음 encoder layer의 input으로 사용함. (encoder layer 수 : 6)
- 모든 encoder layer를 통화하면, BEV feature Bt가 만들어 지고, 3D detection과 map segmentation heat로 3D Bbox와 semantic map을 predict.
3.2 BEV Queries
BEVFormer에서 사용하는 query는 grid 형태이며 learnable parameters로 이루어진다.
이 query를 BEV query라고 부르며, $ Q \in \mathbb{R} ^{H \times W \times C} $ 로 정의된다.
이때, H, W 는 각각 BEV plane의 높이와 너비를 의미한다.
또한, $ Q $ 상에서 $ p = (x,y) $ 에 위치한 쿼리 $ Q_{p} \in \mathbb{R} ^{1 \times C} $ 는 BEV plane 에서 위치 p에 해당하는 grid cell 영역을 의미한다.
BEV plane 상에서 각 grid cell은 real-world size s meter 에 해당한다.
BEV feature의 center는 ego car의 position 에 해당한다.
해당 논문에서는 BEV query Q에 learnable positional embedding을 추가하여 BEVFormer의 input 으로 사용한다.
3.3 Spatial Cross-Attention
Multi camera view (6장)을 input으로 사용하기 때문에, vanilla multi-head attention을 모델로 사용하기엔 computational cost가 너무 높아서 해당 논문은 deformable attention을 기반으로 spatial cross-attention을 구현하였다.
Deformable attention은 Query가 모든 2D feature 영역이 아닌 임의의 관심 영역과만 interaction 이 있도록 설계된 모듈이다.
이 모듈에 대해서는 따로 포스팅하도록 하겠다.
Deformable attention은 2D perception task에 맞게 설계 되었다 보니, 3D scenes에 적용하기 위해 약간의 수정을 했다.
다시 spatial cross-attention 설명으로 넘어가자면,
BEV place 상의 각 query들을 pillar-like query로 옮긴다.
그 다음, 그 pillar에서 $ N_{ref} $ 개의 3D reference points를 뽑아 이 points 들을 2D view들에 project 한다.
하나의 BEV query에서 뽑은 projected 2D points는 일부 view들에만 project가 된 형태가 된다.
이 때, hit views를 $ V_{hit} $ 이라고 표현한다.
그 다음, 이 2D points들을 query $ Q_{p} $ 에서 reference points 로 두고, hit views $ V_{hit} $ 에서 이 reference points 들을 중심으로 feature 를 뽑는다.
마지막으로, 뽑은 feature 들에 대해 weighted sum을 수행한 결과가 spatial cross-attention output 이 된다.
이 과정을 수식으로 나타내면 다음과 같다.

$ i $ 는 camera view의 index, $ j $ 는 reference points의 index, $ N_{ref} $ 는 각 BEV query에서의 total reference points 를,
$ F_{t}^{i} $ 는 i 번째 camera view의 features 를 나타낸다.
각 BEV Query $ Q_{p} $ 에 대해, i 번째 view 에 대한 j 번째 reference point 를 얻기 위해 project function $ P(p, i, j) $ 를 정의한다.
이 project function 이 어떻게 동작하는 지 살펴보자.
우선 grid-shaped query $ Q $ 상에서 $ p=(x, y) $ 위치한 query 한 칸(?)을 $ Q_{p} $ 라고 하면, 이 $ Q_{p} $ 위치에 해당하는 real world location 을 계산한다.
이때, $H, W$ 는 BEV queries의 spatial shape 에 대한 값이고, $s$ 는 BEV’s grid의 resolution size 가 된다.
또한, $ (x’, y’) $ 은 ego car의 위치가 원점일 때의 좌표이다.
본 논문에서 4.2 절 Experimental Settings 에 쓰여 있는 내용에 의하면, BEV Queries 의 크기는 200 * 200 이고, perception ranges 는 [- 51.2 m, 51.2 m] , BEV grid 의 resolution 크기 $s$ 는 0.512 m 라고 한다.
따라서 (1) 식은 ego car 위치를 원점이라고 두었을 때의 상대적인 좌표가 된다.
실제 코드 상에서 역시 아래와 같이 reference points 를 정해줌을 알 수 있다.
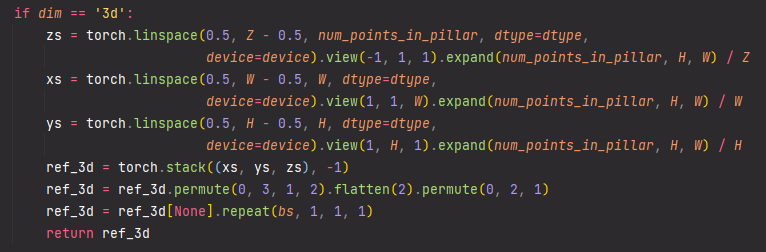
Reference points는 Deformable DETR 논문에 정의된 것 처럼, feature map 상에서의 query 위치 정도로 생각하면 될 것 같다.
어쨌든, 3D space 상에서 $(x’, y’)$ 에 위치한 object는 높이가 각기 다를 것이고, 이 object의 높이 정보는 z축 상의 $ z’ $ 로 표현한다.
$ \lbrace z_{j}’ \rbrace^{N_{ref}}_{j=1} $ predefine 해서 사용함으로써, 각기 다른 높이를 갖는 object 에 대한 정보를 찾을 수 있도록 한다.
따라서, 각 query $ Q_{p} $ 에 대해 pillar 형식의 3D reference points $ \left( x’, y’, z_{j}’ \right)^{N_{ref}}_{j=1} $ 를 구할 수 있다.
이 3D reference points 들을 각 카메라의 projection matrix 에 따라 각기 다른 image views에 project를 한다.
이 연산을 수식으로 표현하면 다음과 같다.
\(P(p, i, j) = (x_{ij}, y_{ij}) \quad where \; z_{ij} \cdot [x_{ij} \; y_{ij} \; 1 ]^{T} \; = \; T_{i} \cdot [x' \; y' \; z_{j}' \; 1]^{T} .\quad \quad (4)\)
위 수식에서 $ P(p, i, j) $ 은 i 번째 view의 2D point를 의미 한다.
수식을 뜯어 보면, j 번째 reference 3D point $ (x’, y’, z_{j}’) $ 와 i번째 카메라의 project matrix $ T_{i} \in \mathbb{R} ^{3 \times 4} $ 를 통해 $ x_{ij}, y_{ij} $ 를 찾아서 2D view 들 중 어디에 project를 할 지 정한다고 볼 수 있다.
3.4 Temporal Self-Attention
본 논문의 저자는 moving object의 velocity를 추론하거나 static images에서 많이 가려진(highly occluded) object를 detection 할 때에 temporal information이 중요하다고 주장한다.
따라서, history BEV feature를 사용하여 temporal information을 뽑기 위해 temporal self-attention 을 디자인 하였다.
현재 시점의 BEV queries $ Q $ 와 $t-1$ 시점의 history BEV features $ B_{t-1} $ 가 있다고 하자.
일단 $ B_{t-1} $ 을 $ Q $ 로 align 을 하는데, 이때 ego-motion 정보를 기반으로 align 한다.
따라서 시점이 다른 BEV query에 대해 같은 위치의 grid를 real-world location 에 맞출 수 있다.
align이 된 BEV feature $B_{t-1}$ 을 $B_{t-1}’$ 이라고 하자.
이때 주의해야 할 점은 $t-1$ 에서 $t$ 로 시간이 지남에 따라, real world 상의 movable objects를 여러 방향으로 움직일 수 있다는 점이다.
이러한 점때문에 다른 시점의 BEV features 간의 동일한 object들에 대해 정확한 assocation을 표현하는 것이 어렵다
따라서, 본 논문에서는 temporal self-attention (TSA) layer를 통해 feature 들 간의 temporal connection을 구축한다.
TSA layer 을 수식으로 표현하면,

여기서 $Q_{p}$ 는 마찬가지로 $ p=(x,y) $ 에 위치한 BEV query를 나타낸다.
또한, vanilla deformable attention 과 달리 TSA 에서 offsets $ \delta p $ 는 $Q$ 와 $B_{t-1}’$을 concatenation 하여 예측을 한다.
각 sequence 의 첫번째 sample 에 대해서는 previous BEV features 가 없으므로, 현재 시점의 BEV query 를 두 개로 복사하여 $ \lbrace Q, Q \rbrace $ 를 input으로 넣는다.
BEV를 stacking 하여 사용하는 기존 논문들과 비교했을 때, BEVFormer의 temporal self-attention은 long temporal dependency 를 더욱 효율적으로 구축할 수 있다.
BEVFormer는 BEV feature들을 여러번 stacking 하는 것보다 previous BEV features 로 부터 temporal information을 뽑으므로, computational cost도 더 적고, disturbing information 문제도 덜 발생한다.
3.5 Applications of BEV Features
BEV feature 는 2D feature map 이기 때문에 3D object detection 외에 map segmentation 에도 활용할 수 있다.
3D Object Detection
따라서, BEVFormer 에서는 2D detector 인 DETR 기반으로 한 end-to-end 3D detection head 를 개발했다.
2D bounding boxes 가 아닌 3D bounding box 와 velocity 를 예측하는 decoder에 single-scale BEV feature를 input으로 하며, bounding box regression 에는 $ L_1 $ loss 를 사용한다.
transformer 기반의 detection head를 사용함으로써 NMS post-processing 없이도 3D bounding box와 velocity 를 예측할 수 있다.

Comments